Dans mes précédents articles, nous avons vu que les nombres étaient partout par nature et que les coïncidences n’était pas toujours si extraordinaires. Cependant, nous n’avons jusqu’à présent considéré que de simples entiers. Il existe pourtant dans l’univers des mathématiques des nombres plus beaux, plus énigmatiques, presque magiques…
Prenons le nombre π : ne vous fait-il pas rêver ? Ses décimales infinies, son nom exotique et ancien, son association à la perfection du cercle… Il y a forcément un peu de magie là-dedans, non ?
Définition : qui est π ?
π est une constante, c’est-à-dire que l’on a donné un nom à un nombre remarquable qui ne varie pas (comme par exemple la constante gravitationnelle (G) ou la vitesse de la lumière (c)).
π est le rapport entre la circonférence d’un cercle et son diamètre.
Prenez n’importe quel cercle, divisez la circonférence par le diamètre, vous obtiendrez toujours la même valeur, une constante que les mathématiciens ont nommée π.
Partout où vous avez un cercle, vous avez π.
Une autre façon de voir les choses est de dire que la circonférence d’une cercle est π fois plus grande que son diamètre.
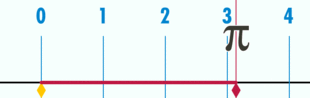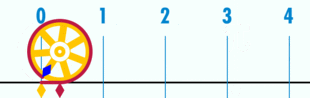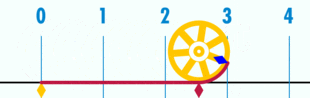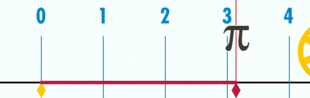
A quoi ça sert ?
Pourquoi donner un nom à ce rapport ?
Parce qu’il simplifie les calculs et que c’est très utile, par exemple, pour trouver l’aire d’un cercle ( π x r2).
Et la magie dans tout ça ?
Après tout, il a des décimales infinies…
… et qui ne se répètent pas. On appelle les nombres de ce genre des nombres irrationnels.
D’autres nombres irrationnels : racine de 2 ou log(2).
J’ai lu qu’il était transcendant
« En mathématiques, un nombre transcendant sur les rationnels est un nombre réel ou complexe qui n’est racine d’aucune équation polynomiale » (Wikipédia)
Il s’agit ici d’une simple propriété mathématique, pas d’une qualité mystique.
D’autres nombres transcendant : sin(1), e, log(3)/log(2)
Ouais, mais un cercle parfait, c’est quand même un peu magique, non ?
Il n’y a rien de plus simple qu’un cercle. La preuve :
Ce que cela nous apprend
On voit souvent de la magie dans les choses que l’on ne comprend pas. Pourtant, une fois qu’on apprend à les connaître, elles deviennent simples.
Cela conclue ma série sur les nombres. N’hésitez pas à utiliser les commentaires si d’autres nombres vous semblent mystérieux.
